[Solved]Pl Maclaurin Series Cosine Loop Vectors 1 Solution Submitted Max Unlimited View Solutions Q37056946
matlab help

![Your Function 1 function [terms, seriesSums, approxRelError, truRelError] maclaurincosine(x, N) 21%Enter the commands for you](https://media.cheggcdn.com/media%2Fc14%2Fc14a8c99-2b44-459e-a0e5-51c697bea72e%2Fimage.png)
 Pl. MacLaurin Series for Cosine (loop and vectors 1 solution submitted (max: Unlimited) View my solutions The cosine function can be approximated by a Maclaurin series expansion as: cos (x) = where.x is in radians. This expression can be used to approximate the cosine of x with increasing accuracy as terms are added to the summation. Code has already been provided to define a function named maclaurinCosine that accepts input values into the following two variables. The variable x accepts a value for l (in radians) for the series approximation of cos(x) The variable N accepts an integer specifying the number of series terms, N, to use in the approximation. – Add code to the function to generate the following four output variables. 1. Generate a column vector of the first N series terms and assign this vector to the variable terms 2. Generate a column vector of the first N series summations. The first summation is I, second is -/2!, third is 1 -x/2!+/4!, and so on. Assign this vector to the output variable seriesSums 3. Generate a column vector of the magnitude (i.e. absolute value) of the approximate relative error values associated with the first N series cmmatione Nnte the “nrevious annroximation” for the first Add code to the function to generate the following four output variables. 1. Generate a column vector of the first N series terms and assign this vector to the variable terms. 2. Generate a column vector of the first N series summations. The first summation is 1, second is 1-x/2!, third is x/2!+a/4!, and so on. Assign this vector to the output variable seriesSums. 3. Generate a column vector of the magnitude (i.e. absolute value) of the approximate relative error values associated with the first N series summations. Note the “previous approximation” for the first value in this vector will be 1 so the number of elements in this vector will be one less than that in the first two outputs. Assign this vector to the output variable approxRelError 4. Generate a column vector of the magnitude of the true relative error values associated with the first V series summations. Use MATLAB’s built-in cosine function to compute the true value for this error calculation. Assign this vector to the output variable truRelError. The first two tests check the results for the second and third series terms respectively to aid in your debugging process. You can also check these values with a hand calculation Note the values of x and N are defined as inputs to the function. Do not overwrite these values in your code. Be sure to assign values to each of the function output variables Your Function 1 function [terms, seriesSums, approxRelError, truRelError] maclaurincosine(x, N) 21%Enter the commands for your function here. 3 s seriesSums ones(1,N) 6 approxRelError ones (1, N) 7 truRelError ones (1, N); 10 ((-1).^k.%.”(2%))/factorial(2%); terms(k)- seriesSums(k) seriesSums (k-1)terms(k); approxReError (k)s abs((seriesSuns(k) seriessums(k-1))/seriessus(k)) %approximates the , 11 13 14 truRelError (k) abs((cos(pi./3)-seriesSums(k))/cos(pi/3)) 15 16 17 end Are the first and second outputs correct for inputs of x – pi/3 and N -2? Variable terms has an incorrect value. Are the first and second outputs correct for inputs of x pi3 and N 3 Variable terms has an incorrect value. Are the error calculations correct for inputs ofx – pi3 and N-3 Variable approxRelError must be of size [2 1]. It is currently of size (3 1]. Check where the variable is assigned a value. Be sure you are taking the absolute value in both error claculations Are all the output variables correct for hidden inputs? Variable terms has an incorrect value. If your code passed the first two tests but not this one it may be that you hard coded the value a/3 into your code and overwrote the value of the input variable x Are the output variables correct for hidden inputs with a negative x value? (Pretest) Variable terms has an incorrect value. Show transcribed image text Pl. MacLaurin Series for Cosine (loop and vectors 1 solution submitted (max: Unlimited) View my solutions The cosine function can be approximated by a Maclaurin series expansion as: cos (x) = where.x is in radians. This expression can be used to approximate the cosine of x with increasing accuracy as terms are added to the summation. Code has already been provided to define a function named maclaurinCosine that accepts input values into the following two variables. The variable x accepts a value for l (in radians) for the series approximation of cos(x) The variable N accepts an integer specifying the number of series terms, N, to use in the approximation. – Add code to the function to generate the following four output variables. 1. Generate a column vector of the first N series terms and assign this vector to the variable terms 2. Generate a column vector of the first N series summations. The first summation is I, second is -/2!, third is 1 -x/2!+/4!, and so on. Assign this vector to the output variable seriesSums 3. Generate a column vector of the magnitude (i.e. absolute value) of the approximate relative error values associated with the first N series cmmatione Nnte the “nrevious annroximation” for the first
Pl. MacLaurin Series for Cosine (loop and vectors 1 solution submitted (max: Unlimited) View my solutions The cosine function can be approximated by a Maclaurin series expansion as: cos (x) = where.x is in radians. This expression can be used to approximate the cosine of x with increasing accuracy as terms are added to the summation. Code has already been provided to define a function named maclaurinCosine that accepts input values into the following two variables. The variable x accepts a value for l (in radians) for the series approximation of cos(x) The variable N accepts an integer specifying the number of series terms, N, to use in the approximation. – Add code to the function to generate the following four output variables. 1. Generate a column vector of the first N series terms and assign this vector to the variable terms 2. Generate a column vector of the first N series summations. The first summation is I, second is -/2!, third is 1 -x/2!+/4!, and so on. Assign this vector to the output variable seriesSums 3. Generate a column vector of the magnitude (i.e. absolute value) of the approximate relative error values associated with the first N series cmmatione Nnte the “nrevious annroximation” for the first Add code to the function to generate the following four output variables. 1. Generate a column vector of the first N series terms and assign this vector to the variable terms. 2. Generate a column vector of the first N series summations. The first summation is 1, second is 1-x/2!, third is x/2!+a/4!, and so on. Assign this vector to the output variable seriesSums. 3. Generate a column vector of the magnitude (i.e. absolute value) of the approximate relative error values associated with the first N series summations. Note the “previous approximation” for the first value in this vector will be 1 so the number of elements in this vector will be one less than that in the first two outputs. Assign this vector to the output variable approxRelError 4. Generate a column vector of the magnitude of the true relative error values associated with the first V series summations. Use MATLAB’s built-in cosine function to compute the true value for this error calculation. Assign this vector to the output variable truRelError. The first two tests check the results for the second and third series terms respectively to aid in your debugging process. You can also check these values with a hand calculation Note the values of x and N are defined as inputs to the function. Do not overwrite these values in your code. Be sure to assign values to each of the function output variables Your Function 1 function [terms, seriesSums, approxRelError, truRelError] maclaurincosine(x, N) 21%Enter the commands for your function here. 3 s seriesSums ones(1,N) 6 approxRelError ones (1, N) 7 truRelError ones (1, N); 10 ((-1).^k.%.”(2%))/factorial(2%); terms(k)- seriesSums(k) seriesSums (k-1)terms(k); approxReError (k)s abs((seriesSuns(k) seriessums(k-1))/seriessus(k)) %approximates the , 11 13 14 truRelError (k) abs((cos(pi./3)-seriesSums(k))/cos(pi/3)) 15 16 17 end Are the first and second outputs correct for inputs of x – pi/3 and N -2? Variable terms has an incorrect value. Are the first and second outputs correct for inputs of x pi3 and N 3 Variable terms has an incorrect value. Are the error calculations correct for inputs ofx – pi3 and N-3 Variable approxRelError must be of size [2 1]. It is currently of size (3 1]. Check where the variable is assigned a value. Be sure you are taking the absolute value in both error claculations Are all the output variables correct for hidden inputs? Variable terms has an incorrect value. If your code passed the first two tests but not this one it may be that you hard coded the value a/3 into your code and overwrote the value of the input variable x Are the output variables correct for hidden inputs with a negative x value? (Pretest) Variable terms has an incorrect value. Show transcribed image text Pl. MacLaurin Series for Cosine (loop and vectors 1 solution submitted (max: Unlimited) View my solutions The cosine function can be approximated by a Maclaurin series expansion as: cos (x) = where.x is in radians. This expression can be used to approximate the cosine of x with increasing accuracy as terms are added to the summation. Code has already been provided to define a function named maclaurinCosine that accepts input values into the following two variables. The variable x accepts a value for l (in radians) for the series approximation of cos(x) The variable N accepts an integer specifying the number of series terms, N, to use in the approximation. – Add code to the function to generate the following four output variables. 1. Generate a column vector of the first N series terms and assign this vector to the variable terms 2. Generate a column vector of the first N series summations. The first summation is I, second is -/2!, third is 1 -x/2!+/4!, and so on. Assign this vector to the output variable seriesSums 3. Generate a column vector of the magnitude (i.e. absolute value) of the approximate relative error values associated with the first N series cmmatione Nnte the “nrevious annroximation” for the first
Add code to the function to generate the following four output variables. 1. Generate a column vector of the first N series terms and assign this vector to the variable terms. 2. Generate a column vector of the first N series summations. The first summation is 1, second is 1-x/2!, third is x/2!+a/4!, and so on. Assign this vector to the output variable seriesSums. 3. Generate a column vector of the magnitude (i.e. absolute value) of the approximate relative error values associated with the first N series summations. Note the “previous approximation” for the first value in this vector will be 1 so the number of elements in this vector will be one less than that in the first two outputs. Assign this vector to the output variable approxRelError 4. Generate a column vector of the magnitude of the true relative error values associated with the first V series summations. Use MATLAB’s built-in cosine function to compute the true value for this error calculation. Assign this vector to the output variable truRelError. The first two tests check the results for the second and third series terms respectively to aid in your debugging process. You can also check these values with a hand calculation Note the values of x and N are defined as inputs to the function. Do not overwrite these values in your code. Be sure to assign values to each of the function output variables
Your Function 1 function [terms, seriesSums, approxRelError, truRelError] maclaurincosine(x, N) 21%Enter the commands for your function here. 3 s seriesSums ones(1,N) 6 approxRelError ones (1, N) 7 truRelError ones (1, N); 10 ((-1).^k.%.”(2%))/factorial(2%); terms(k)- seriesSums(k) seriesSums (k-1)terms(k); approxReError (k)s abs((seriesSuns(k) seriessums(k-1))/seriessus(k)) %approximates the , 11 13 14 truRelError (k) abs((cos(pi./3)-seriesSums(k))/cos(pi/3)) 15 16 17 end
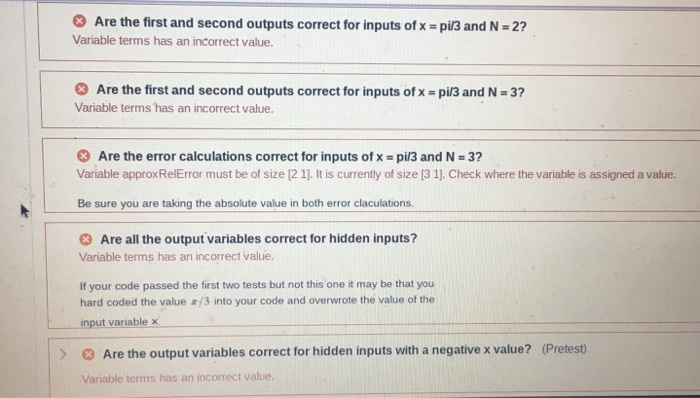
Are the first and second outputs correct for inputs of x – pi/3 and N -2? Variable terms has an incorrect value. Are the first and second outputs correct for inputs of x pi3 and N 3 Variable terms has an incorrect value. Are the error calculations correct for inputs ofx – pi3 and N-3 Variable approxRelError must be of size [2 1]. It is currently of size (3 1]. Check where the variable is assigned a value. Be sure you are taking the absolute value in both error claculations Are all the output variables correct for hidden inputs? Variable terms has an incorrect value. If your code passed the first two tests but not this one it may be that you hard coded the value a/3 into your code and overwrote the value of the input variable x Are the output variables correct for hidden inputs with a negative x value? (Pretest) Variable terms has an incorrect value.
Expert Answer
Answer to Pl. MacLaurin Series for Cosine (loop and vectors 1 solution submitted (max: Unlimited) View my solutions The cosine fun… . . .
OR

