[Solved] Using Matlab Please Help Priovide Code Answer Problem Clear Clear Variables M 1 Mass Kg K Q37177266

using matlab please help priovide code to answer problem

clear all; % clear all variables

m=1; %mass[kg]
k = 4; % spring constant [N/m]

omega0 = sqrt(k/m);

y0 =-0.8; v0 = -0.3; % initial conditions
[t,Y] = ode45(@f,[0,10],[y0,v0],[],omega0); % solve for0<t<10

y = Y(:,1); v = Y(:,2); % retrieve y, v from Y
figure(1); plot(t,y,’bo-‘,t,v,’r+-‘);% time series for y and vgridon; axistight;%—————————————————
function dYdt = f(t,Y,omega0); % function defining the DE
y = Y(1); v = Y(2);
dYdt=[ v ; – omega0^2*y ];
end

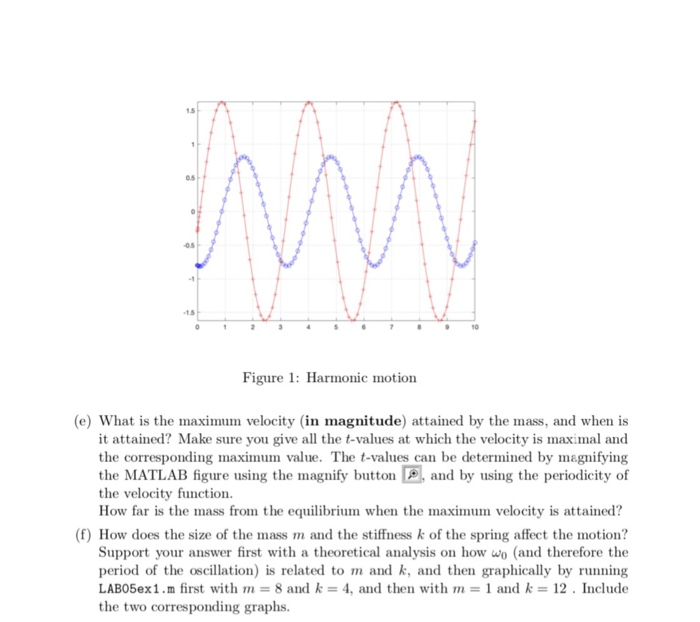
clear all: n-1; % nass [kg] k.4; % spring constant [N/ ] omega。. sqrt (k/s); yo .-0.8; vo . -o.3; % initial conditions [t,T] . ode45 (cf. [O. 10], [yo,v0],[],oaega0); % clear all variables % solve for 0<t<10 figure ( 1 ) ; plot ( t .y.’bo-,,t,v,’r+-‘);% grid on; axis tight for tine series y and function dYdt ” f(t,Y,onegao); % function defining the DE end Note that the paraneter wp was passed as an argument to ode45 rather than set to its value 2 directly in the function f. The advantage is that its value can easily be changed in the driver part of the program rather than in the function, for example wben multiple plots with different values of w need to be compared in a single MATLAB figure wi NOTE for the following exercises, just like for all the other lab reportss otherrise specified, include in your lab rort all M-iles, igures, MATLAB Inpat commands, the core sponding output, and the answers to the questions I. From the graph in Fig 1 answer the follkowing questions (a) Which curve represents yy(t)? How do you knO (b) What is the period of the motion? Aswer this question first grapbically (by reading the period from the graph) and then analytically (by finding the period wing) (c) We say that the mass comes to rest if, after a certain time, the position of the mass remains within an arbitrary small distance from the equilibeim position Will the mass ever come to rest? Why (d) What is the amplitude of the oscillations for y Figure 1: Harmonic motion 15 05 1.5 10 Figure 1: Harmonic motion (e) What is the maximum velocity (in magnitude) attained by the mass, and when is sure you give all the t-values at which the velocity is maximal and the corresponding maximum value. The t-values can be determined by magnifying the MATLAB figure using the magnify buttonand by using the periodicity of the velocity function How far is the mass from the equilibrium when the maximum velocity is attained? (f) How does the size of the mass m and the stiffness k of the spring affect the motion? Support your answer first with a theoretical analysis on how wo (and therefore the period of the oscillation) is related to m and k, and then graphically by running LAB05ex1.m first with m = 8 and k = 4, and then with m 1 and k 12 . Include the two corresponding graphs. Show transcribed image text clear all: n-1; % nass [kg] k.4; % spring constant [N/ ] omega。. sqrt (k/s); yo .-0.8; vo . -o.3; % initial conditions [t,T] . ode45 (cf. [O. 10], [yo,v0],[],oaega0); % clear all variables % solve for 0

Expert Answer

---

Answer to using matlab please help priovide code to answer problem clear all; % clear all variables m=1; %mass[kg] k = 4; % spring… . . .