[Solved]04 02 Given 1 First System One Solution 3x 4y 1 5 6x Y 9 2 Second System Solution 3x 4y 1 Q37186171
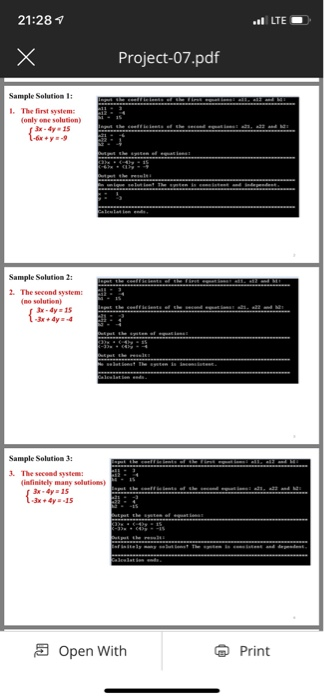04/02 Given: 1. The first system: (only one solution) 3x -4y 1!5 -6x +y-9 2. The second system: (no solution) 3x -4y 1!5 3x +4y -4 3. The second system: (infinitely many solutions) 3x -4y 1!5 3x4y -15 Requirements: a) Your code needs to be able to use “Cramer’s Rule” (see page 5 & 6) to solve ANY system of two-linear equations! (5 points) b) Three systems are given above. You need to find solutions for all c) You need to output each system of equations. (5 points each) d) You need to output the solution for each system:. If there is no solution, print “No solution! The system is inconsistent.” 2. If there are infinitely many solutions, print “Infinitely many solutions! The system is consistent and dependent.” 3. If there is a solution, print it out. Also, print “An unique solution! The system is consistent and independent.” (10 points each). See samples of outputs shown on the next three pages. 21:28 LTE Project-07.pdf Sample Solution 1: . The first system: (only one solution) Sample Solution 2 2. The second system: (no solutien) Ix-4y 15 Sample Solution 3: 3. The second system ininitely many selutionns 3x-4y 15 x4y-15 Print a Open With Show transcribed image text 04/02 Given: 1. The first system: (only one solution) 3x -4y 1!5 -6x +y-9 2. The second system: (no solution) 3x -4y 1!5 3x +4y -4 3. The second system: (infinitely many solutions) 3x -4y 1!5 3x4y -15 Requirements: a) Your code needs to be able to use “Cramer’s Rule” (see page 5 & 6) to solve ANY system of two-linear equations! (5 points) b) Three systems are given above. You need to find solutions for all c) You need to output each system of equations. (5 points each) d) You need to output the solution for each system:. If there is no solution, print “No solution! The system is inconsistent.” 2. If there are infinitely many solutions, print “Infinitely many solutions! The system is consistent and dependent.” 3. If there is a solution, print it out. Also, print “An unique solution! The system is consistent and independent.” (10 points each). See samples of outputs shown on the next three pages.
21:28 LTE Project-07.pdf Sample Solution 1: . The first system: (only one solution) Sample Solution 2 2. The second system: (no solutien) Ix-4y 15 Sample Solution 3: 3. The second system ininitely many selutionns 3x-4y 15 x4y-15 Print a Open With
Expert Answer
Answer to 04/02 Given: 1. The first system: (only one solution) 3x -4y 1!5 -6x +y-9 2. The second system: (no solution) 3x -4y 1!5… . . .
OR
